Geschatte leestijd: 6 minutes

In dit artikel bespreken we wat compound interest precies is, vervolgens ontleden we de formule en als laatste bespreken we hoe we samengestelde interest kunnen gebruiken in ons dagelijks leven en in onze beleggingen.
Inhoud
Compound interest is simpelweg interest op interest, ofwel ‘rente op rente’. De Nederlandse vertaling luidt dan ook ‘samengestelde interest’. Dit fenomeen zorgt voor een exponentieel verloop van een totale som. Het begrip is bijvoorbeeld toepasselijk bij langjarige investeringen en het herinvesteren van dividenden.
Compound interest (samengestelde interest)
Interest in deze context is een percentage dat we verdienen of betalen op een bepaalde som geld. Bij het principe van interest op interest verdienen we in periode 2 ook interest op de interest van periode 1. Hieronder maken we dit inzichtelijk.
| Tijd | Totaal | Interest |
| Periode 1 | 100 | 5% |
| Periode 2 | 105 | 5% |
| Periode 3 | 110,25 | 5% |
| Periode 4 | 115,76 | 5% |
In periode 1 sparen we 100 euro, waar we 5% rente op krijgen. In periode 2 staat er dus 105 euro op onze rekening. Hier krijgen we vervolgens nogmaals 5% rente op. We krijgen dus extra interest, namelijk 5% van de vorige 5 euro, dus 0,25 euro.
De keerzijde van de medaille
Samengestelde interest beleggen kan ook enorm tegen ons werken. De rekensom zoals hierboven gaat immers ook op voor schulden. Op deze manier kan een persoon of bedrijf in moeilijkheden zeer snel in een neerwaartse spiraal belanden en dit niet meer te boven komen.
De formule
Uit ons bovenstaande voorbeeld kunnen we de volgende formule afleiden.
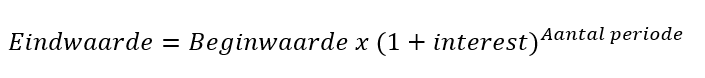
Na 10 jaar is onze 100 euro dus gegroeid naar € 155,13. Een totaalrendement van 55,13%. 155,13 = 100 x (1 + 0,05)^10.
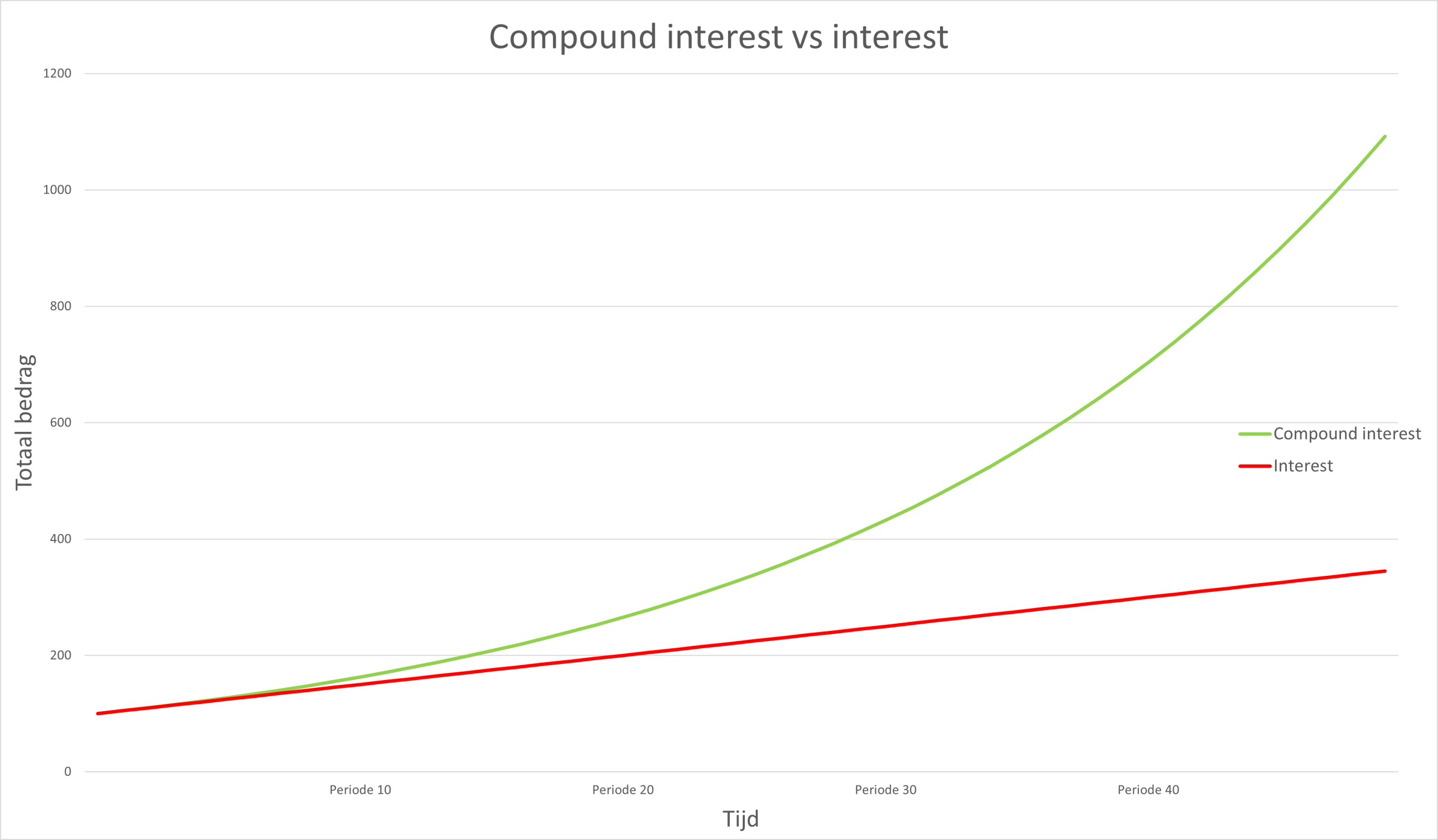
Stel dat we onze samengestelde interest telkens naar een andere rekening hadden overgeschreven dan bedroeg het rendement 50% (10 x 5 euro interest). Op 50 jaar wordt dit verschil nog groter. Na 50 jaar beschikken we over een bedrag van €1092,13 uitgaande van samengestelde interest. Zonder dit effect komt het bedrag uit op €350. Grafisch ziet dit er als volgt uit:
De compound annual growth rate (CAGR)
We kunnen de formule omvormen en vervolgens onze eigen eindwaarde kiezen. Zo bepalen we als belegger of trader ons jaarlijks doelrendement. Stel dat een 20-jarige belegger start met €10.000 en een eindwaarde van €50.000 wil op diens 30e verjaardag. Het benodigde jaarlijks rendement is dan 17,46%. We noemen dit de compound annual growth rate en deze is te berekenen met onderstaande formule:
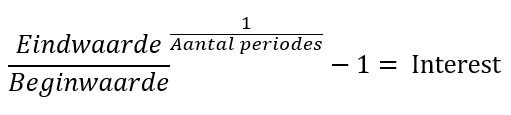
De 72-regel
Om te berekenen wanneer de beginwaarde van een investering verdubbelt in het geval van compound interest, kunnen we gebruikmaken van de 72- regel. Daarbij delen we 72 door ons interestpercentage. In ons eerste voorbeeld gebruiken we 5%. Dus 72 / 5 is 14,4 jaar tegen onze 100 euro verdubbeld. Dat is ook in de grafiek te zien. In het geval van ‘gewone’ interest verdubbelt de investering na 20 jaar.
Zoals gezegd werkt compound interest in twee richtingen. Ook bij schulden geldt het principe. Een actueel voorbeeld is de recente inflatie in Nederland en België. In oktober 2022 werd een inflatie van 14,3% en 12,27% gerapporteerd. Als deze inflatie doorzet in de komende jaren dan heeft dit grote consequenties voor een tegoeden op renteloze spaarrekeningen. Mocht een Belgische spaarder kapitaal houden op een spaarrekening (renteloos) zal de rekening in koopkracht halveren in 72/12,27 = 5,87 jaar. De koopkracht van de Nederlandse spaarder halveert in 5,03 jaar.
Samengestelde interest bij de buy and hold beleggingsstrategie
Via samengestelde interest kunnen we ook een schatting maken voor langetermijninvesteringen zoals extra pensioen. Het principe wordt dan “rendement op rendement”. Aan de hand van een voorbeeld laten we zien hoe dit werkt.
Een voorbeeld
Een belegger belegt een initieel bedrag van 1.000 euro in een MSCI World ETF. Hierna legt deze belegger ieder jaar 1.000 euro in.
Om onze berekening solide te maken, hanteren we een aantal aannames. De afgelopen 50 jaar steeg de globale aandelenmarkt 10% per jaar. Dit trekken we verder voor de volgende 50 jaar. Vervolgens corrigeren we het nominale rendement met een gemiddelde inflatie van 2% en bekomen we een reëel rendement van 8%.
| Totaal | Leeftijd |
| € 1000 | 20 jaar |
| € 16 645,49 | 30 jaar |
| € 50 422,92 | 40 jaar |
| € 123 345,87 | 50 jaar |
| € 280 781,04 | 60 jaar |
| € 619 671,77 | 70 jaar |
In deze tabel is het exponentieel effect zeer duidelijk zichtbaar. In de eerste 10 jaar halen we 6 545,49 euro uit beleggingen terwijl dat in de laatste 10 jaar meer dan 228 890,73 euro is.
Na 40 jaar heeft de belegger 50.000 euro ingelegd. Dit is verwaarloosbaar als we kijken naar het totaal rendement van 569 671,77 euro. Deze berekening kunnen we zien als een basisscenario. Naarmate een carrière vordert zullen we logischerwijs ook meer gaan investeren. Omgekeerd is het ook waar dat sommige periodes lastiger kunnen zijn om zich aan het plan te houden.
Dit rekenvoorbeeld maakt duidelijk dat het zin heeft om zo vroeg mogelijk te beginnen met geld opzij leggen. Mocht de belegger uit ons voorbeeld 10 jaar later beginnen, dat is de uiteindelijke opbrengst bij pensionering de helft van het resultaat in de berekening.
Dividend herbeleggen
Het principe van dividenden herbeleggen heeft dezelfde werking als het zojuist behandelde voorbeeld. Mochten we een dividend van 3% ontvangen na belastingen en we beleggen ons cash geld in hetzelfde aandeel dan ontvangen we het volgende jaar 3% extra op de vorige 3%. En zo schiet ook hier de exponentiële werking in gang.


