Geschatte leestijd: 9 minuten
In dit artikel leggen we u uit wat historische volatiliteit is, wat implied volatility precies is en hoe u dit kunt interpreteren. Daarnaast bespreken we de termen volatility skew, term structure, volatility smile en implied volatility rank.
Bent u op zoek naar een broker om opties te handelen, klik dan hier.
Uitleg historische volatiliteit
Het begrip volatiliteit heeft betrekking op beweeglijkheid. De historische volatiliteit, afgekort HV, slaat op de gerealiseerde beweging. Dit is niets ander dan de koersuitslagen uit het verleden, waarbij dit in het TWS Handelsplatform wordt getoond voor een periode van 30 dagen.
De historische volatiliteit zegt dus iets over het verleden en niet direct iets over de toekomst. Alsnog is het belangrijk om te zien hoe de koersontwikkelingen in de afgelopen periode zijn geweest. Dit vormt in veel gevallen namelijk de leidraad voor de verwachte toekomstige koersontwikkelingen.
De onderstaande grafiek toont de AEX-index met daaronder een weergave van de historische volatiliteit. Wat mogelijk als eerste opvalt, is dat de historische volatiliteit wordt weergegeven als percentage. Dit is de gerealiseerde beweging van de afgelopen 30 dagen omgerekend op jaarbasis. De beweging in de afgelopen 30 handelsdagen is daarmee omgerekend op jaarbasis uitgekomen op ongeveer 23,8%. Eind maart, toen de uitslagen nog aanzienlijk groter waren, kwam de volatiliteit uit boven de 28%. Daarentegen was het in september 2021 juist relatief rustig op de financiële markten, waarmee de volatiliteit op ongeveer 11% stond.
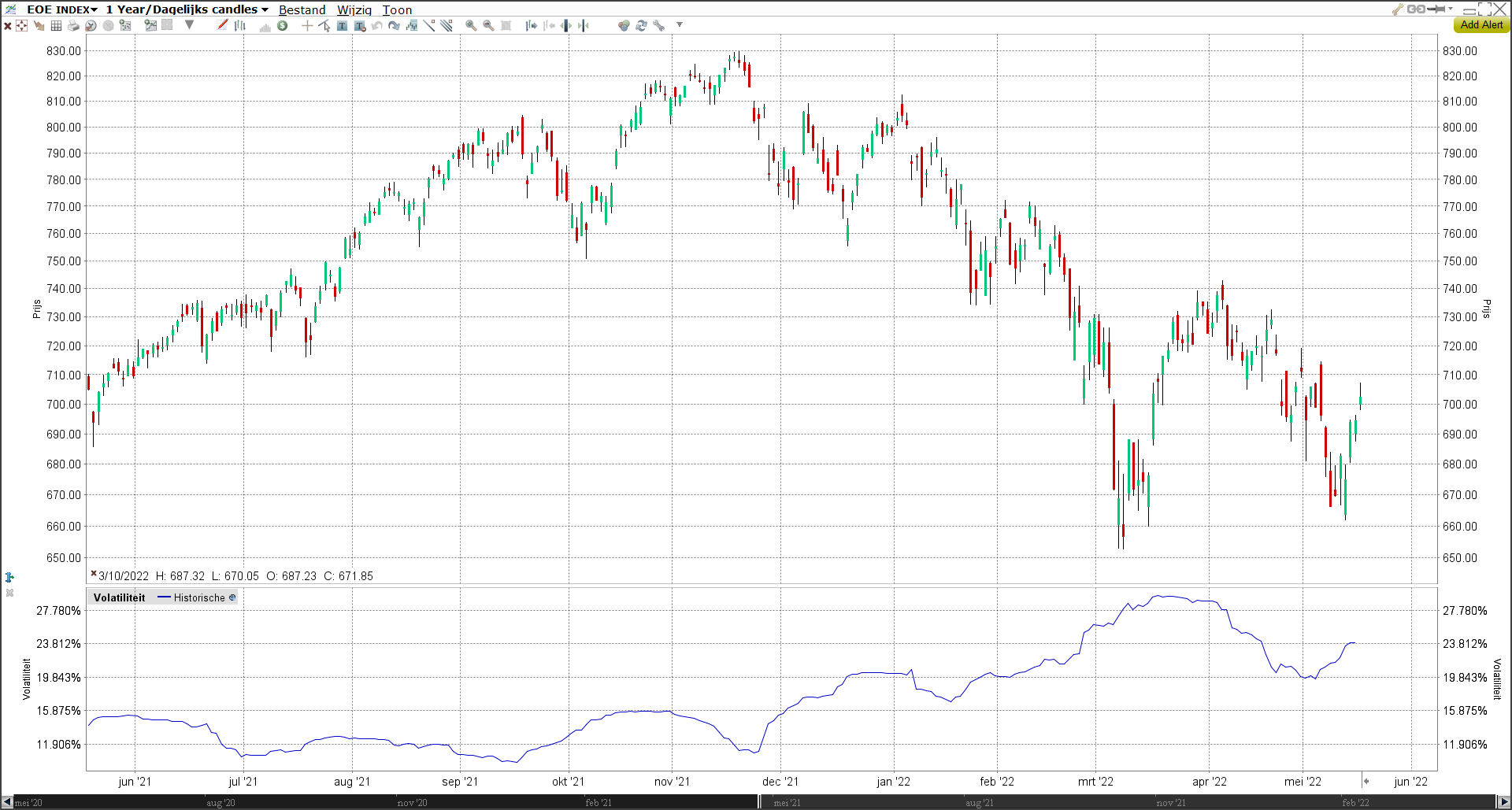
Dat de volatiliteit in september op 11% bedroeg, heeft verder geen directe voorspellende waarde over de markt. Het is enkel een weergave van hoe beweeglijk de AEX in die periode is geweest. Daarbij is het wel logisch dat wanneer de beweging in een bepaalde periode beperkt is geweest, dit als uitgangspunt wordt gebruikt voor de verwachte toekomstige beweging.
Dus wanneer de historische volatiliteit laag is, dan is dit in het algemeen ook het geval voor de verwachte volatiliteit. Simpel gesteld: tussen de historische volatiliteit en de verwachte volatiliteit bestaat een positieve correlatie. Neemt de beweging op de beurzen toe, dan geldt dit op een soortgelijke manier voor de beweging die verwacht wordt. Kortom, de historische volatiliteit en de implied volatiliteit zijn van groot belang voor elkaar.
Wat is implied volatility precies?
Waar de historische volatiliteit echter betrekking heeft op het verleden, is de implied volatility de verwachting van de toekomst. In het Black-Scholes optiemodel is de implied volatility de ontbrekende variabele. De andere variabelen, waaronder de koers van de onderliggende waarde, de looptijd van de optie, de uitoefenprijs en de rente, zijn gegeven.
Aan de hand van de implied volatility wordt de prijs van een optie bepaald. Dit is de verwachte beweeglijkheid van de onderliggende waarde tot expiratiedatum. Overigens is er nog één variabele die niet vast staat, namelijk de verwachte dividenden. In grote lijnen staat dit uiteraard vast, al kan een verhoging of verlaging van het dividend van grote invloed zijn op de optiepremies.
De implied volatility is dus cruciaal voor het prijzen van opties. Deze waarde wordt door de markt bepaald. Daarmee bedoel ik dat het onder andere een kwestie van vraag en aanbod is. Is er vanuit de markt veel vraag naar bijvoorbeeld putopties, dan neemt de implied volatility van deze opties toe. De prijs van de opties zal namelijk stijgen naarmate de vraag groot is. Uiteindelijk zijn het market makers die continu prijzen van opties afgeven. Zij zijn de liquidity providers die bied- en laatkoersen op het scherm laten zien en daarmee de implied volatility van de opties bepalen.
Volatiliteit als percentage
Zoals eerder kort aangestipt wordt zowel de historische volatiliteit als implied volatility weergegeven als percentage. Dit percentage heeft betrekking op de volatiliteit op jaarbasis. Om de volatiliteit terug te rekenen van jaarbasis naar dagbasis, deelt u deze door 16. Nu is natuurlijk de vraag hoe we aan 16 komen.
In een jaar zitten iets meer dan 250 handelsdagen. Wanneer we voor het gemak uitgaan van 256 handelsdagen, dan is de volatiliteit op dagbasis terug te rekenen door gebruik te maken van de wortel van het aantal handelsdagen. De wortel van 256 is 16. Op deze manier kunt u dit terugrekenen van jaarbasis naar dagbasis.
Interpretatie van de implied volatility
De implied volatility van een optie is een weergave van de verwachte beweeglijkheid van de onderliggende waarde tot expiratiedatum van de optie. Bij een implied volatiliteit van 16% bedraagt de volatiliteit op dagbasis 1%. Dit is gebaseerd op één standaarddeviatie. Dit houdt in dat 68,2% (tweemaal 34,1%, omdat de beweging zowel positief als negatief kan uitpakken) van de handelsdagen een beweging van 1% of minder wordt verwacht. Voor de overige 31,8% van de handelsdagen worden grotere uitslagen verwacht. Dit is eenvoudig uit te leggen aan de hand van de onderstaande normale verdeling.
Op basis van de normale verdeling is de verwachting dat op 27,2% (tweemaal 13,6%) van de handelsdagen, de beweging tussen één en twee keer de standaarddeviatie zal zijn. In dit voorbeeld komt dat neer op een beweging tussen de 1% en 2% en de -1% en -2%. Op 4,2% (tweemaal 2,1%) van de handelsdagen wordt een beweging tussen de 2% en 3% of -2% en -3% verwacht van de aandelenkoers. Tot slot wordt op 0,2% van de handelsdagen een beweging groter dan 3% of -3% verwacht.
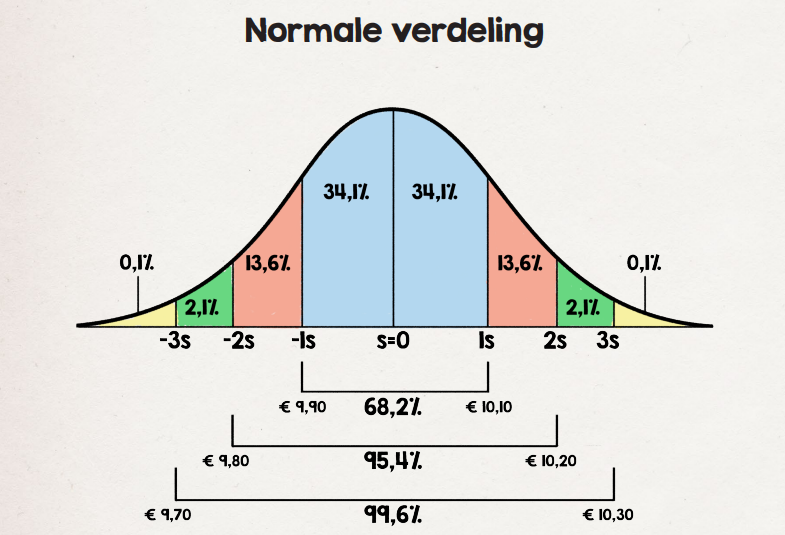
Als voorbeeld neem ik een aandeel dat noteert op € 10, waarbij de at-the-money calloptie een volatiliteit heeft van 16%. In het bovenstaande plaatje is te zien dat de optie is geprijsd met een verwachte zekerheid van ruim 99% dat de koers van het aandeel bij het slot van de volgende handelsdag tussen € 9,70 en € 10,30 noteert.
Volatility skew
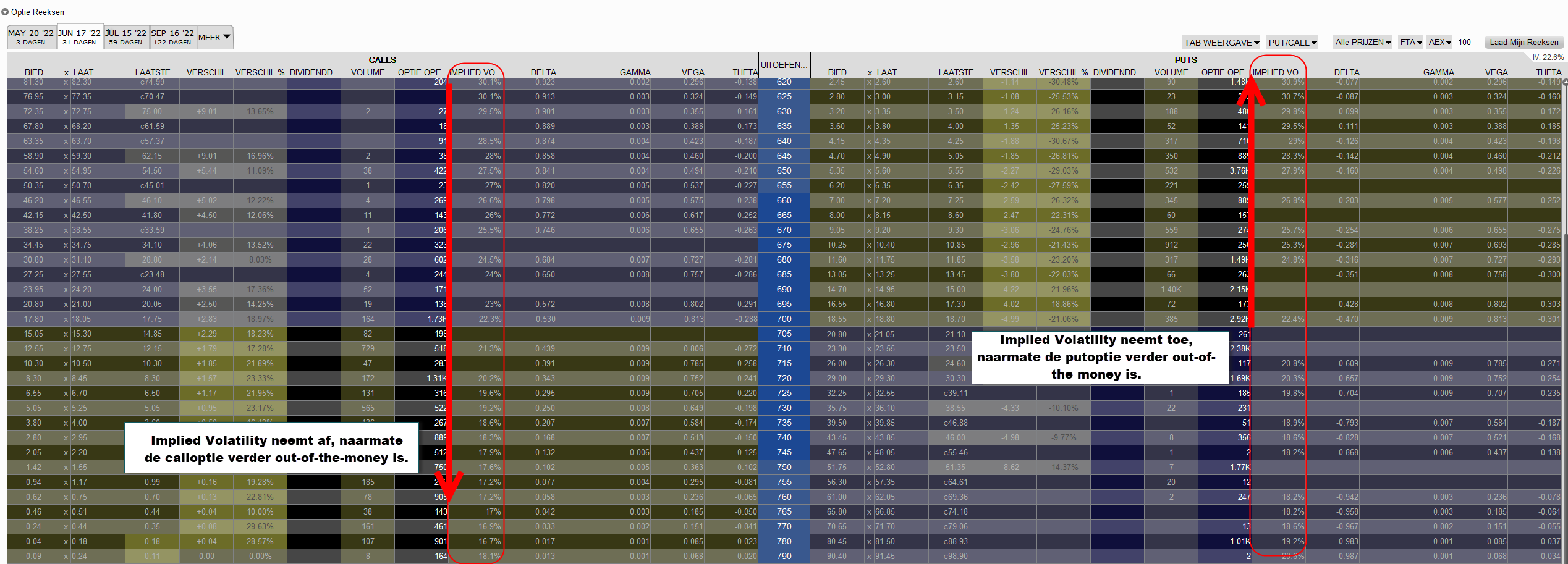
Opties met eenzelfde looptijd en een verschillende uitoefenprijs worden niet aan de hand van dezelfde implied volatility geprijsd. Daarmee wordt bedoeld dat de opties onderling gewaardeerd worden tegen een verschillende hoeveelheid van beweeglijkheid. Zo wordt een at-the-money putoptie over het algemeen tegen een lagere implied volatility geprijsd dan een out-of-the-money putoptie. Dit fenomeen, ontstaan na de crash in 1987, wordt omschreven als de volatility skew.
Voor een optiebelegger is het belangrijk om te begrijpen wat het gevolg is van de volatility skew bij het maken van handelsbeslissingen. Wanneer out-of-the-money putopties geprijsd worden tegen een hogere implied volatility, dan zijn deze opties relatief duur tegenover bijvoorbeeld at-the-money putopties.
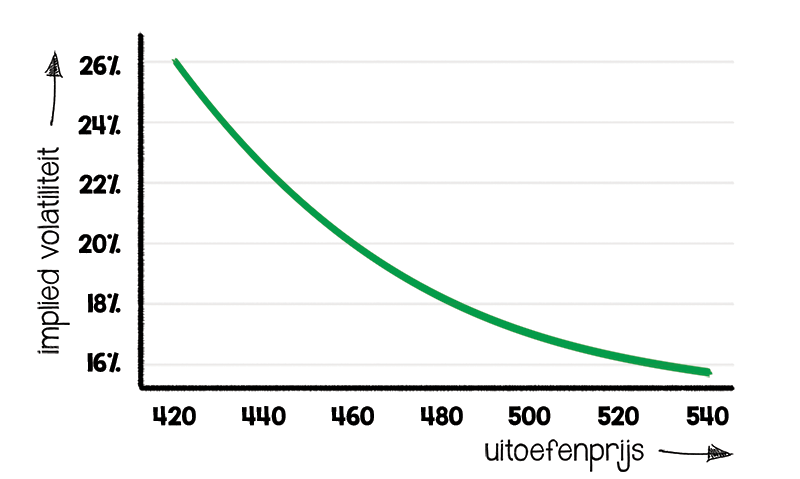
De out-of-the-money putopties met een relatief hoge implied volatility kunnen worden vergeleken met een brandverzekering op een huis. De kans dat brand uitbreekt, is zeer klein. Maar áls dit gebeurt, is de schade enorm. Dit kunnen we doortrekken naar de beleggingswereld. Wanneer de beurs hard naar beneden gaat, zoals bij een crash, dan bieden juist deze out-of-the-money putopties bescherming tegen verliezen op uw portefeuille.
Term structure
Waar de volatility skew het verschil in implied volatility per optie met eenzelfde expiratiedatum weergeeft, geeft de term structure het verschil in implied volatility weer per optie met dezelfde uitoefenprijs en verschillende expiratiedata.
Opties met dezelfde uitoefenprijzen en verschillende expiratiedata hebben een verschil in implied volatility en worden hierdoor anders geprijsd. Dit effect is voornamelijk te verklaren aan hoe de markt beweging in de onderliggende waarde op basis van toekomstige gebeurtenissen inschat. Zo is het gangbaar dat de implied volatility toeneemt richting de kwartaalcijfers. Nadat de markt de cijfers heeft ontvangen en de koersbeweging is geweest, neemt de implied volatility weer af.
Voor kortlopende opties beweegt de implied volatility meer dan bij langer lopende opties. De term structure van de volatiliteit geeft daarmee de relatie weer van de implied volatility en de looptijd tot expiratie. Op deze manier interpreteren optiehandelaren of bepaalde optiemaanden goedkoop of juist duur zijn. Zo is het niet ongebruikelijk dat de zomermaanden tegen lagere implied volatility worden geprijsd dan bijvoorbeeld september en oktober. Het is in de zomer over het algemeen rustig op de financiële markten en de verwachte koersuitslagen zijn daarmee kleiner.
De onderstaande tabel toont de implied volatility van at-the-money AEX opties voor expiratiedata van 10 – tot 100 dagen. In dit fictieve scenario is de implied volatility sterk opgelopen. Over een langere periode is de verwachting dat de beweeglijkheid iets afneemt en dat de markten in rustiger vaarwater terecht komen.
| Expiratie | Implied volatility |
| 10 dagen | 19,55% |
| 40 dagen | 19,73% |
| 70 dagen | 18,10% |
| 100 dagen | 17,58% |
Tijdens schokken loopt de implied volatility het snelst op bij de kortst lopende opties. Hoe korter een optie loopt, des te groter is de invloed van de huidige marktbeweging op de implied volatility van de optie aangezien de expiratiedatum het dichtst bij ligt. De implied volatility geeft de verwachte beweging weer tot expiratiedatum en wanneer de looptijd nog kort is, heeft een onverwachte beweging het meeste invloed op de implied volatility.
In sommige jaren is vooral het omgekeerde beeld zichtbaar. De opties met de kortste looptijd worden in deze situatie geprijsd tegen de laagste volatiliteit, terwijl de langer lopende opties een hogere volatiliteit hebben. De beurs beweegt dan vaak langzaam omhoog met van tijd tot tijd neerwaartse bewegingen.
Volatility smile
Een concept dat nauw verwant is aan dat van de volatility skew is de volatility smile. Het is een situatie waarbij de at-the-money opties een lagere implied volatility hebben dan de out-of-the money en in-the-money opties. In deze situatie neemt de implied volatility van puts en calls toe naarmate de uitoefenprijs verder afwijkt van de huidige prijs van de onderliggende waarde. Dit wordt getoond in de onderstaande grafiek waar we kunnen zien dat de volatiliteit van juli, augustus en september afnemen naarmate ze dichter bij de at-the-money strike komen en toenemen naarmate ze zich verder van de at-the-money strike bewegen. We spreken van een volatility smile door de vorm die de grafiek weergeeft.
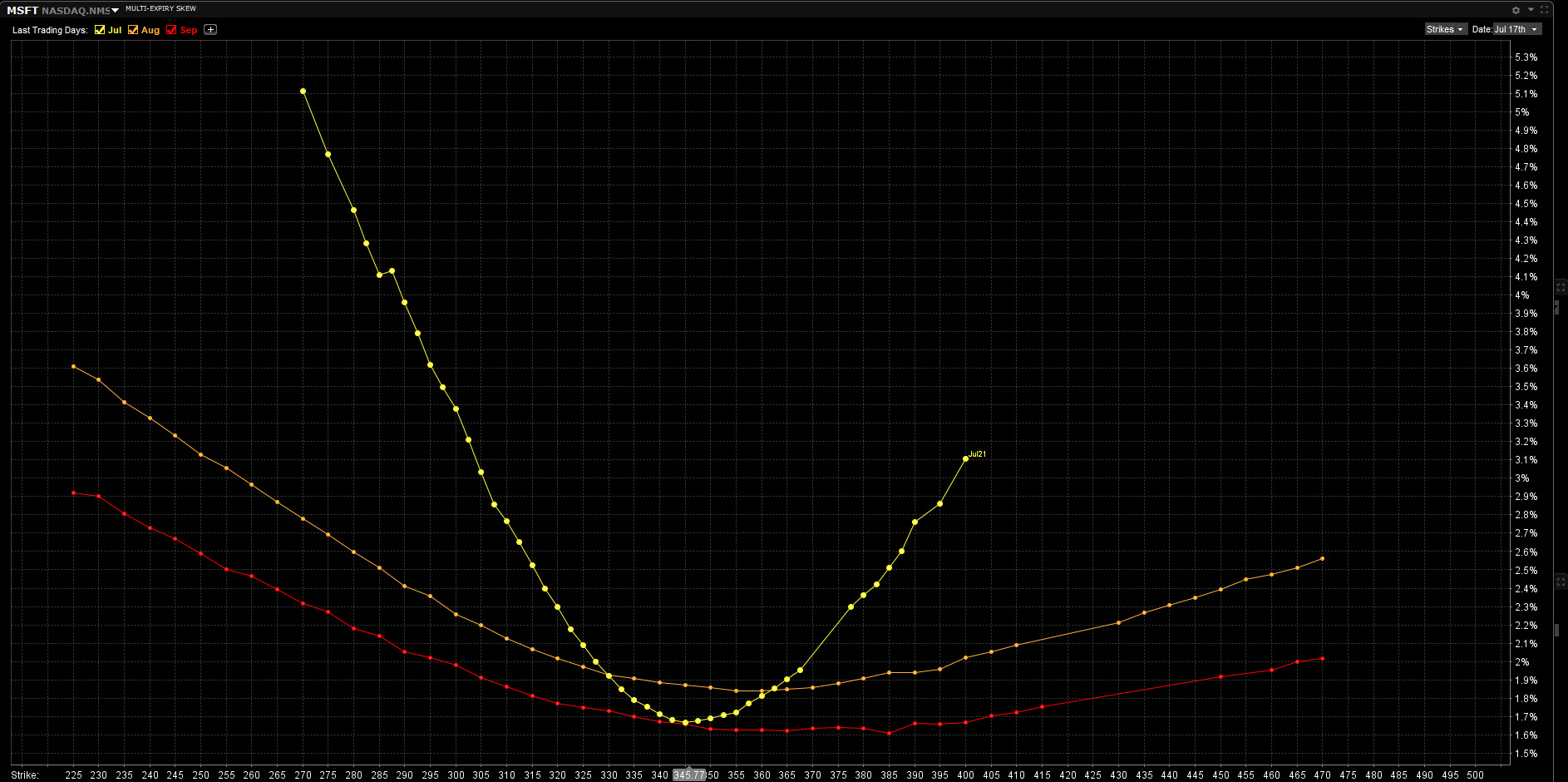
Wat het fenomeen van de volatility smile kan verklaren, is het feit dat op de aandelenmarkt de meeste beleggers long posities aanhouden. Als ze hun posities willen beschermen met behulp van optiestrategieën kan gegrepen worden naar een protective put en de covered call. De protective put zal in de meeste gevallen gepaard gaan met de aankoop van een put optie die niet at-the-money is. Het verkopen van een covered call gaat gepaard met de verkoop van een call die niet at-the-money is.
Implied volatility rank
De IV-rank oftewel implied volatility rank is een meting die de huidige implied volatility van een bepaalde onderliggende waarde weergeeft ten opzichte van de implied volatility van de afgelopen 52 weken. Als de implied volatility rank gelijk is aan nul dan betekent dit dat het huidige niveau van de implied volatilit het laagste niveau heeft bereikt van het afgelopen jaar. Als de implied volatility rank gelijk is aan 100, betekent dit dat de implied volatility het hoogste niveau heeft bereikt van het afgelopen jaar.
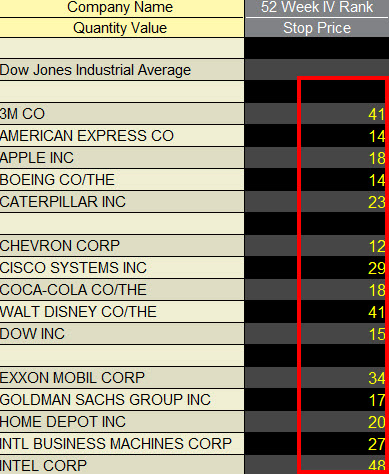
De implied volatility rank helpt ons te begrijpen of de implied volatility van een bepaald instrument hoog of laag is. Wanneer de implied volatility hoog is, kan het nuttig zijn om een optiestrategie te volgen die inspeelt op een dalende volatiliteit, terwijl bij een lage implied volatility, het juist nuttig kan zijn om een optiestrategie te volgen die inspeelt op een volatiliteit die toeneemt.
Opties kopen en schrijven via LYNX
Via LYNX kunt u zeer voordelig beleggen in opties. Met enkele muisklikken handelt u eenvoudig in alle Europese en Amerikaanse aandelenopties en indexopties. Tevens heeft u de beschikking over de beste trader tools, zoals de OptieTrader en kunt u optiecombinaties in zijn geheel naar de beurs versturen.
--- ---
--- (---%)Displaying the --- grafiek
Displaying today's chart
